[Algorithms | C++] Bubble sort : 버블 정렬

버블 정렬(Bubble sort) 알고리즘의 개념

• 서로 인접한 두 원소를 검사하여 정렬하는 알고리즘
  • 인접한 2개의 레코드를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환한다.
• 선택 정렬과 기본 개념이 유사하다.

버블 정렬(Bubble sort) 알고리즘의 예제

• 배열에 7, 4, 5, 1, 3이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해 보자.

• 

• 1회전
  • 첫 번째 자료 7을 두 번째 자료 4와 비교하여 교환하고, 두 번째의 7과 세 번째의 5를 비교하여 교환하고, 세 번째의 7과 네 번째의 1을 비교하여 교환하고, 네 번째의 7과 다섯 번째의 3을 비교하여 교환한다. 이 과정에서 자료를 네 번 비교한다. 그리고 가장 큰 자료가 맨 끝으로 이동하므로 다음 회전에서는 맨 끝에 있는 자료는 비교할 필요가 없다.
• 2회전
  • 첫 번째의 4을 두 번째 5와 비교하여 교환하지 않고, 두 번째의 5와 세 번째의 1을 비교하여 교환하고, 세 번째의 5와 네 번째의 3을 비교하여 교환한다. 이 과정에서 자료를 세 번 비교한다. 비교한 자료 중 가장 큰 자료가 끝에서 두 번째에 놓인다.
• 3회전
  • 첫 번째의 4를 두 번째 1과 비교하여 교환하고, 두 번째의 4와 세 번째의 3을 비교하여 교환한다. 이 과정에서 자료를 두 번 비교한다. 비교한 자료 중 가장 큰 자료가 끝에서 세 번째에 놓인다.
• 4회전
  • 첫 번째의 1과 두 번째의 3을 비교하여 교환하지 않는다.

C++로 구현한 버블 정렬 (Bubble sort)

이전에 작성한 양방향 링크드 리스트의 코드를 재활용

void DoubleList::BubbleSort() {
	Node *Current(NULL);
	for (int i = 0; i < CountNode() - 1; i++) {
		Current = Head;
		for (int j = 0; j < CountNode() - (i + 1); j++) {
			if (Current->getData() > Current->getRlink()->getData()) {
				Node *tmp = Current->getRlink();
				if (tmp == NULL) {
					return;
				}
				if (Current == Head) {
					Head = tmp;
					if (tmp == Tail) {
						Tail = Current;
					}
					else if(tmp != Tail)
					{
						tmp->getRlink()->setLlink(Current);
					}
				}
				else if (tmp == Tail) {
					Tail = Current;
					Current->getLlink()->setRlink(tmp);
				}
				else {
					tmp->getRlink()->setLlink(Current);
					Current->getLlink()->setRlink(tmp);
				}
				Current->setRlink(tmp->getRlink());
				tmp->setLlink(Current->getLlink());

				Current->setLlink(tmp);
				tmp->setRlink(Current);

				Current = tmp;
			}
			Current = Current->getRlink();
		}
	}
}

버블 정렬(Bubble sort) 알고리즘의 특징

• 장점
  • 구현이 매우 간단하다.
• 단점
  • 순서에 맞지 않은 요소를 인접한 요소와 교환한다.
  • 하나의 요소가 가장 왼쪽에서 가장 오른쪽으로 이동하기 위해서는 배열에서 모든 다른 요소들과 교환되어야 한다.
  • 특히 특정 요소가 최종 정렬 위치에 이미 있는 경우라도 교환되는 일이 일어난다.
• 일반적으로 자료의 교환 작업(SWAP)이 자료의 이동 작업(MOVE)보다 더 복잡하기 때문에 버블 정렬은 단순성에도 불구하고 거의 쓰이지 않는다.

버블 정렬(Bubble sort)의 시간복잡도

시간복잡도를 계산한다면

• 비교 횟수
  • 최상, 평균, 최악 모두 일정
  • n-1, n-2, … , 2, 1 번 = n(n-1)/2
• 교환 횟수
  • 입력 자료가 역순으로 정렬되어 있는 최악의 경우, 한 번 교환하기 위하여 3번의 이동(SWAP 함수의 작업)이 필요하므로 (비교 횟수 - 3) 번 = 3n(n-1)/2
  • 입력 자료가 이미 정렬되어 있는 최상의 경우, 자료의 이동이 발생하지 않는다.
• T(n) = O(n^2)

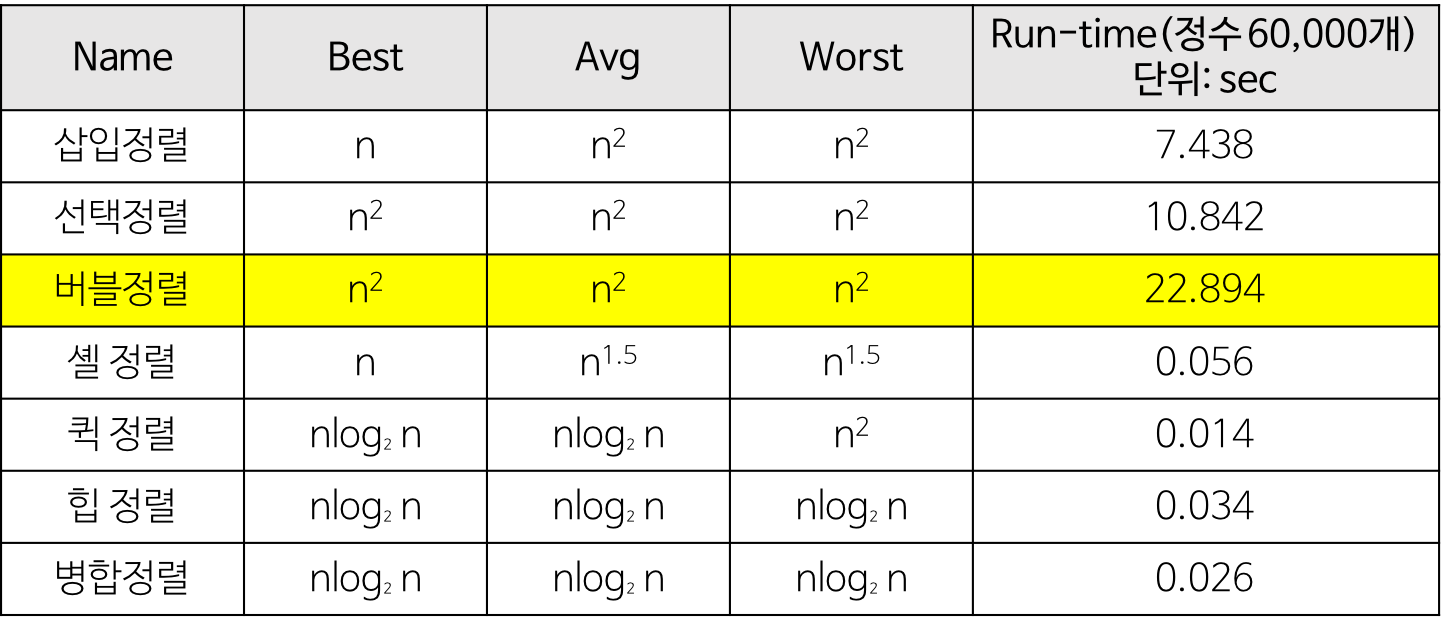
정렬 알고리즘 시간복잡도 비교

• 단순(구현 간단)하지만 비효율적인 방법
  • 삽입 정렬, 선택 정렬, 버블 정렬
• 복잡하지만 효율적인 방법
  • 퀵 정렬, 힙 정렬, 합병 정렬, 기 수 정렬

References

• 버블 정렬 - 위키백과