[Algorithms | C++] Quick sort : 퀵 정렬

퀵 정렬(Quick sort) 알고리즘의 개념 요약

• ‘찰스 앤터니 리처드 호어(Charles Antony Richard Hoare)’가 개발한 정렬 알고리즘
• 퀵 정렬은 불안정 정렬 에 속하며, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬 에 속한다.
• 분할 정복 알고리즘의 하나로, 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법
  • 합병 정렬(merge sort)과 달리 퀵 정렬은 리스트를 비균등하게 분할한다.
• 분할 정복(divide and conquer) 방법
  • 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다.
  • 분할 정복 방법은 대개 순환 호출을 이용하여 구현한다.
• 과정 설명
  1. 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 피벗(pivot) 이라고 한다.
  2. 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다. (피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)
  3. 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
     • 분할된 부분 리스트에 대하여 순환 호출 을 이용하여 정렬을 반복한다.
     • 부분 리스트에서도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분 리스트로 나누는 과정을 반복한다.
  4. 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복한다.
     • 리스트의 크기가 0이나 1이 될 때까지 반복한다.
• 

퀵 정렬(Quick sort) 알고리즘의 구체적인 개념

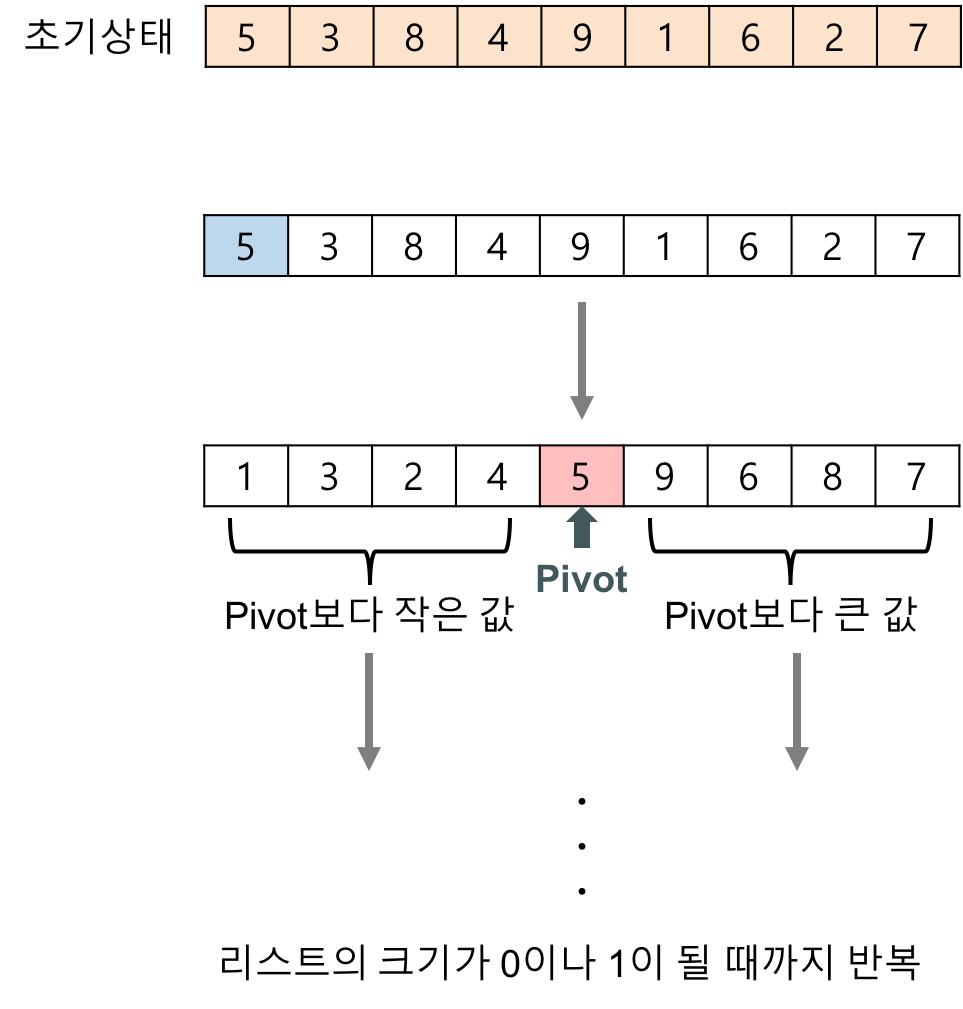
• 하나의 리스트를 피벗(pivot)을 기준으로 두 개의 비균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법이다.
• 퀵 정렬은 다음의 단계들로 이루어진다.
  • 분할(Divide): 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열(피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)로 분할한다.
  • 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
  • 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.
  • 순환 호출이 한번 진행될 때마다 최소한 하나의 원소(피벗)는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.
• 

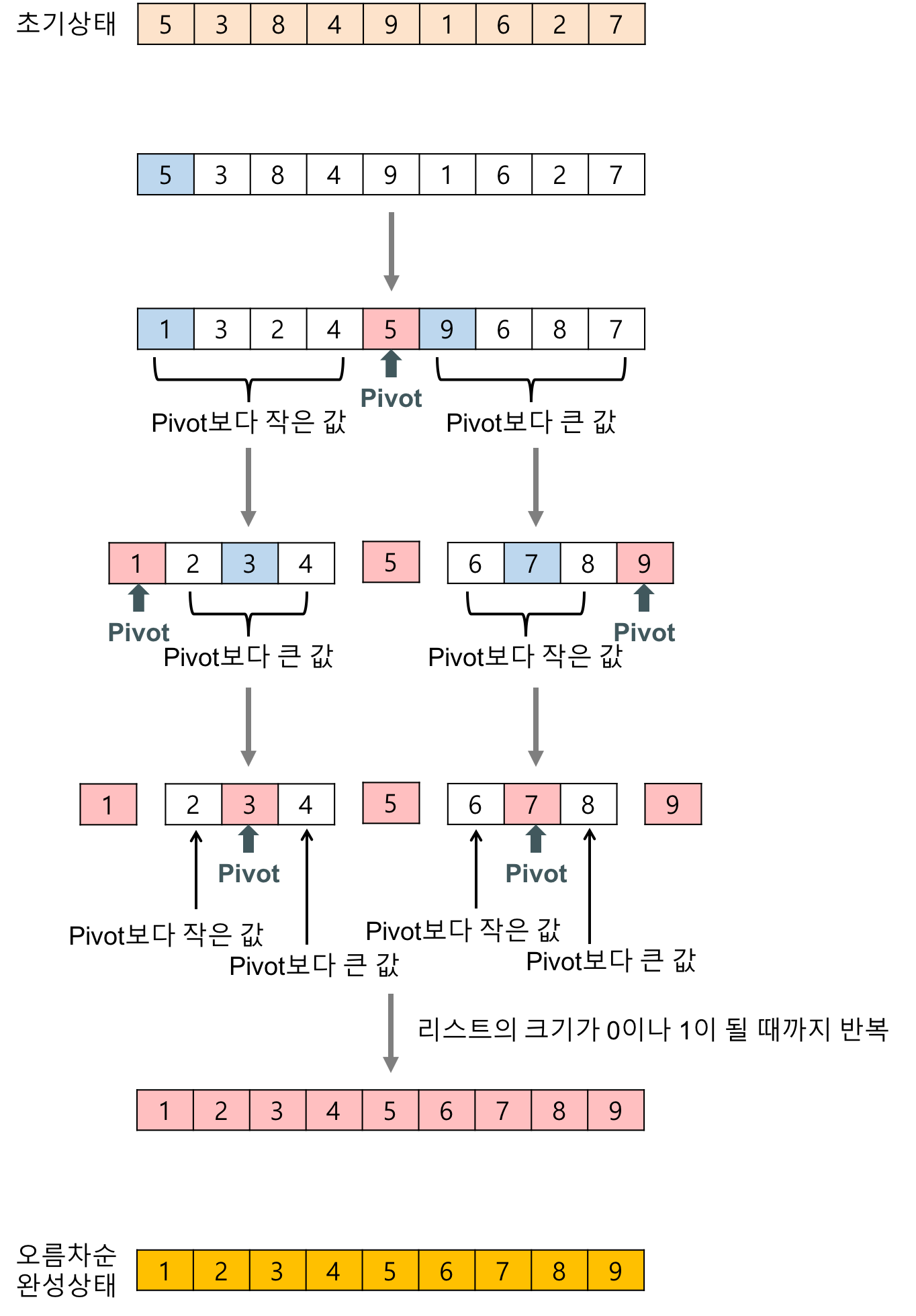
퀵 정렬(Quick sort) 알고리즘의 예제

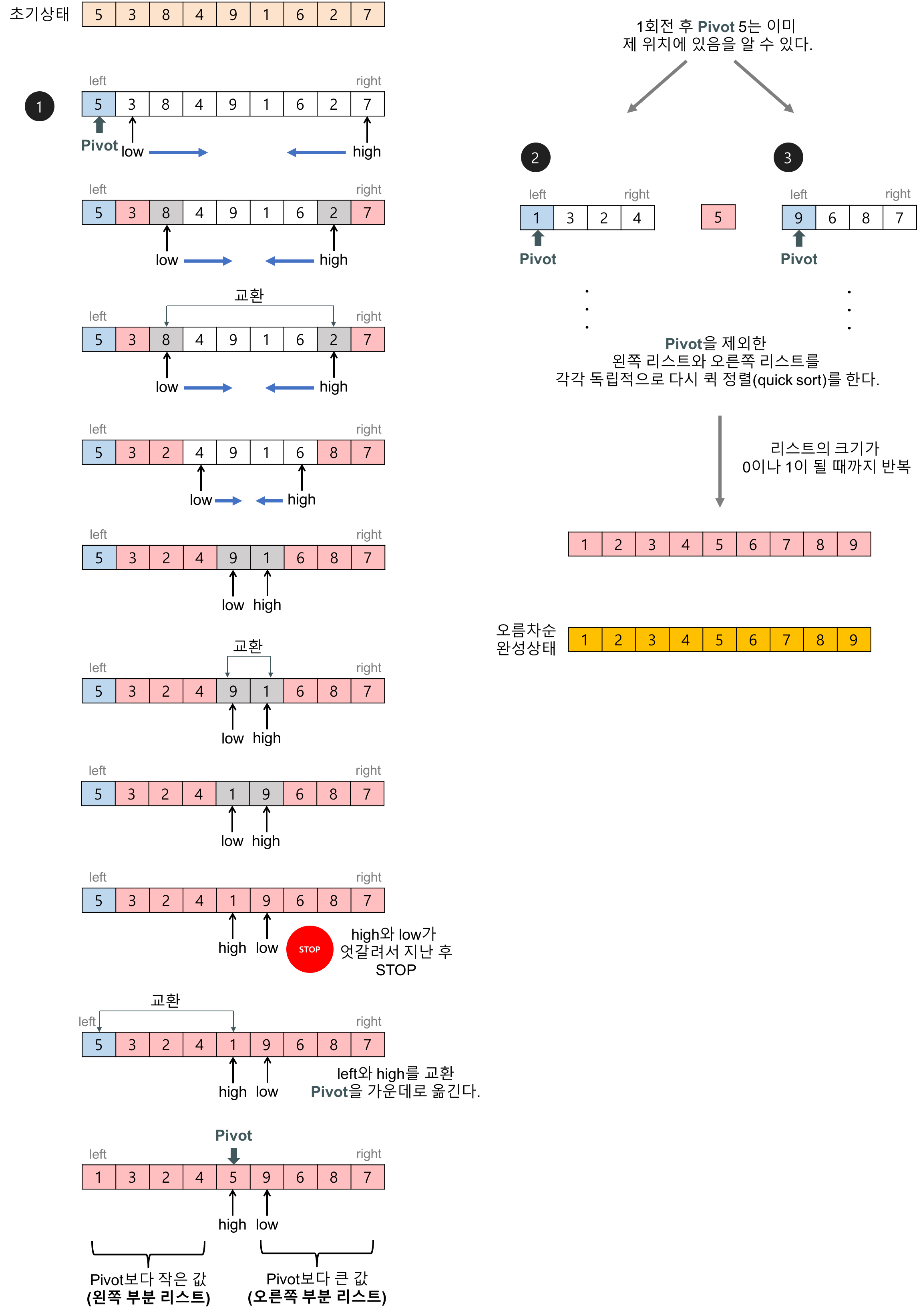
• 배열에 5, 3, 8, 4, 9, 1, 6, 2, 7이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해 보자.
• 퀵 정렬에서 피벗을 기준으로 두 개의 리스트로 나누는 과정(c언어 코드의 partition 함수의 내용)

• 

• 피벗 값을 입력 리스트의 첫 번째 데이터로 하자. (다른 임의의 값이어도 상관없다.)
• 2개의 인덱스 변수(low, high)를 이용해서 리스트를 두 개의 부분 리스트로 나눈다.
• 1회전: 피벗이 5인 경우,
  1. low는 왼쪽에서 오른쪽으로 탐색해가다가 피벗보다 큰 데이터(8)을 찾으면 멈춘다.
  2. high는 오른쪽에서 왼쪽으로 탐색해가다가 피벗보다 작은 데이터(2)를 찾으면 멈춘다.
  3. low와 high가 가리키는 두 데이터를 서로 교환한다.
  4. 이 탐색-교환 과정은 low와 high가 엇갈릴 때까지 반복한다.
• 2회전: 피벗(1회전의 왼쪽 부분리스트의 첫 번째 데이터)이 1인 경우,
  • 위와 동일한 방법으로 반복한다.
• 3회전: 피벗(1회전의 오른쪽 부분리스트의 첫 번째 데이터)이 9인 경우,
  • 위와 동일한 방법으로 반복한다.

C++로 구현한 퀵 정렬 (Quick sort)

이전에 작성한 양방향 링크드 리스트의 코드를 재활용

void DoubleList::QuickSort(int Left, int Right)
{
	if (Left < Right) {
		int index = Partition(Left, Right);

		QuickSort(Left, index - 1);
		QuickSort(index + 1, Right);
	}
}

int DoubleList::Partition(int Left, int Right)
{
	int first = Left;
	int pivot = ArrangeNode(first)->getData();
	++Left;
	while (Left <= Right)
	{
		while (ArrangeNode(Left)->getData() <= pivot && Left < Right) {
			++Left;
		}
		while (ArrangeNode(Right)->getData() > pivot && Left <= Right) {
			--Right;
		}
		if (Left < Right) {
			Swap(ArrangeNode(Left), ArrangeNode(Right));
		}
		else {
			break;
		}
	}
	Swap(ArrangeNode(first), ArrangeNode(Right));

	return Right;
}

퀵 정렬(quick sort) 알고리즘의 특징

• 장점
  1. 속도가 빠르다.
     • 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
  2. 추가 메모리 공간을 필요로 하지 않는다.
     • 퀵 정렬은 O(log n)만큼의 메모리를 필요로 한다.
• 단점
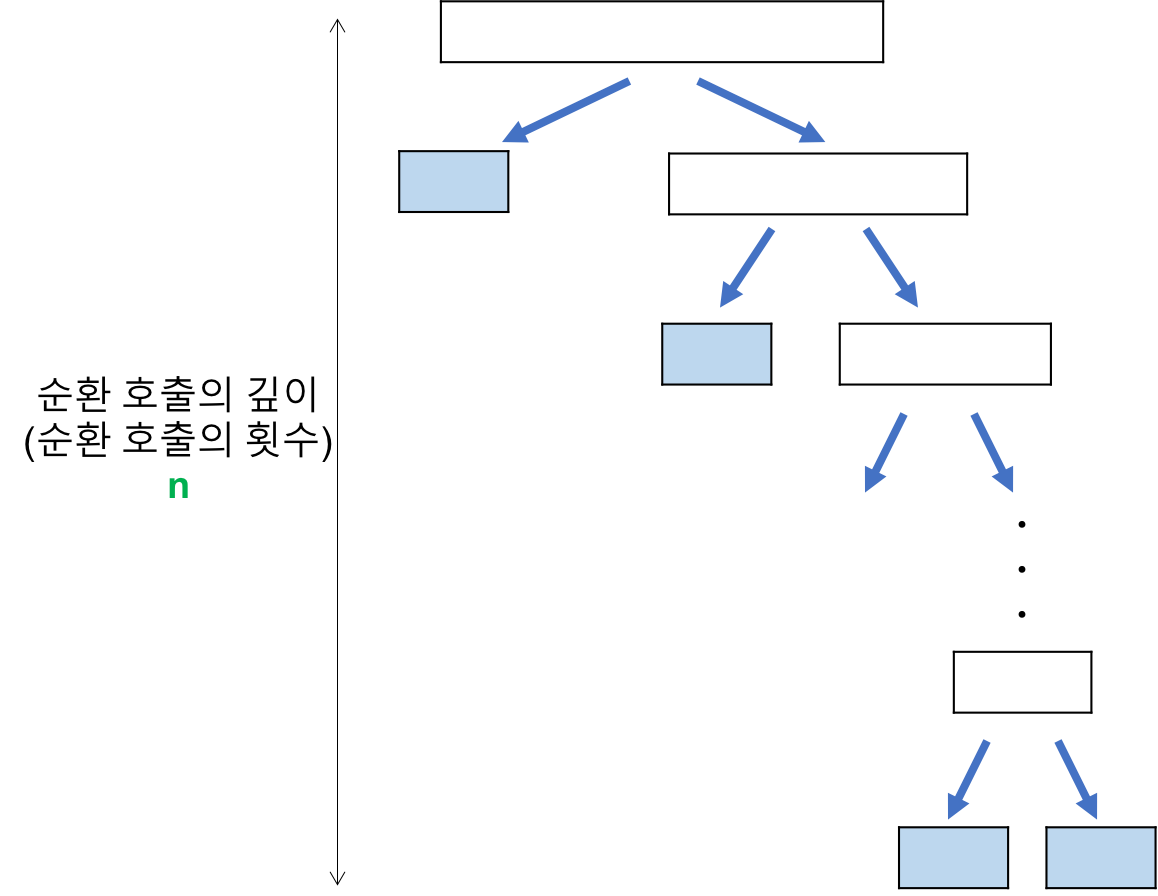
  1. 정렬된 리스트에 대해서는 퀵 정렬의 불균형 분할에 의해 오히려 수행시간이 더 많이 걸린다.
• 퀵 정렬의 불균형 분할을 방지하기 위하여 피벗을 선택할 때 더욱 리스트를 균등하게 분할할 수 있는 데이터를 선택한다.
  • EX) 리스트 내의 몇 개의 데이터 중에서 크기순으로 중간 값(medium)을 피벗으로 선택한다.

퀵 정렬(quick sort)의 시간복잡도

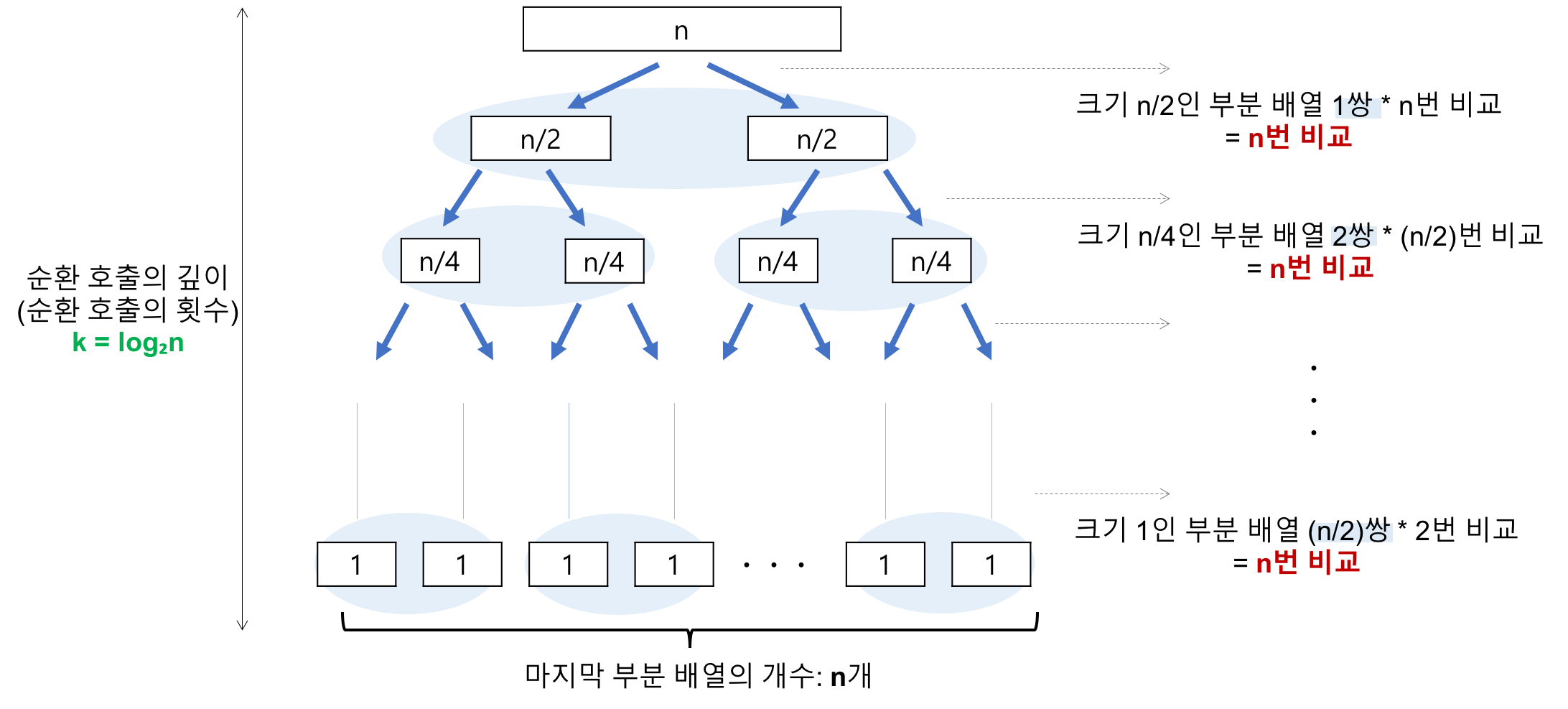
• 최선의 경우
  • 비교 횟수
    • 
    • 순환 호출의 깊이
      • 레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다. 이것을 일반화하면 n=2^k의 경우, k(k=log₂n)임을 알 수 있다.
      • k=log₂n
    • 각 순환 호출 단계의 비교 연산
      • 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
      • 평균 n번
    • 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = nlog₂n
  • 이동 횟수
    • 비교 횟수보다 적으므로 무시할 수 있다.
  • 최선의 경우 T(n) = O(nlog₂n)
• 최악의 경우
  • 리스트가 계속 불균형하게 나누어지는 경우 (특히, 이미 정렬된 리스트에 대하여 퀵 정렬을 실행하는 경우)
  • 
  • 비교 횟수
    • 순환 호출의 깊이
      • 레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, 순환 호출의 깊이는 n임을 알 수 있다.
      • n
    • 각 순환 호출 단계의 비교 연산
      • 각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
      • 평균 n번
    • 순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = n^2
  • 이동 횟수
    • 비교 횟수보다 적으므로 무시할 수 있다.
  • 최악의 경우 T(n) = O(n^2)
• 평균
  • 평균 T(n) = O(nlog₂n)
  • 시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
  • 퀵 정렬이 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗 들이 추후 연산에서 제외되는 특성 때문이다.

정렬 알고리즘 시간복잡도 비교

• 단순(구현 간단)하지만 비효율적인 방법
  • 삽입 정렬, 선택 정렬, 버블 정렬
• 복잡하지만 효율적인 방법
  • 퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬

References

• 퀵 정렬 - 위키백과